| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 데이터 엔지니어링
- sql
- linux
- S3
- 가상환경
- redshift
- 데브코스
- Go
- dockerfile
- PYTHON
- 데이터 파이프라인
- 운영체제
- TIL
- airflow
- HADOOP
- 데이터엔지니어링
- AWS
- 데이터베이스
- Docker
- 종류
- TCP
- airflow.cfg
- 컴퓨터 네트워크
- 데이터 웨어하우스
- 컴퓨터네트워크
- 파이썬
- 정리
- 자료구조
- http
- Django
- Today
- Total
홍카나의 공부방
[자료구조] Heap의 개념과 연산, 시간 복잡도 본문
Heap
힙(Heap)은 가장 큰 값 혹은 가장 작은 값을 바로 꺼낼 수 있도록 만든 자료구조다. 여기서 단순한 정렬 알고리즘처럼 전체 key 값에 대한 오름차순이나 내림차순 정렬이 목표가 아니라는 점을 유의하자. 스택, 큐와 내부 구조를 비교한다면 아래와 같다.
- 스택 : LIFO
- 큐 : FIFO
- 힙 : 가장 큰 값(Maxheap), 가장 작은 값(Minheap)
힙은 필요한 만큼만 정렬이 되어 있다. 여기서 필요한 만큼이라 하면, 본래의 목적인 가장 큰 값 찾기를 지킬 수 있는 만큼만 정렬이 되어 있다는 것이다. 그래서 정렬이 주 목적이라면 다른 자료구조를 이용할 것을 권장한다.
구현은 Maxheap으로 진행한다. Minheap의 경우 Maxheap 구현을 약간만 바꿔주면 구현할 수 있다. 그리고 Tree 구조로 힙을 나타낼 수 있는데, 실제 구현은 배열로도 가능하다.
힙의 삽입
특별한 언급을 하지 않는 이상, 여기서 말하는 힙은 모두 맥스힙(Maxheap)을 이야기한다. 트리로 나타낸 힙에서, 가장 큰 값은 항상 root에 위치한다. 또한, 완전 이진 트리 구조를 유지할 수 있게끔 새로운 값이 추가되어야 한다. 이 제약 조건들을 계속 지킬 수 있도록 새로운 노드를 삽입해야 한다. 로직은 아래 그림과 같다.

1. 항상 가장 큰 값은 root 노드에 유지해야 한다.
2. 만약 새로운 값을 가진 노드가 삽입될 경우, 원래 삽입되어야 하는 자리(그러니까, 완전 이진트리 구조를 유지하면서 맨 마지막 자식 노드)의 부모 노드들과 비교를 시작한다. 위 그림에서는 8의 자리의 부모 노드인 2와 비교를 한다.

3. 부모 노드와 값을 비교한 뒤, 부모 노드 key값 보다 크다면 부모 노드의 값을 자식 노드 위치로 내리고(복사하고), 부모가 여럿이라면 그 부모를 계속 타고 타고 올라간다. 그리고 들어가야 할 위치에 새로운 값을 대입한다.
[ Swap으로 구현을 할 수도 있겠으나, 여기서는 기존 값을 복사하고 새로운 값을 대입하는 방법을 선택한다. ]
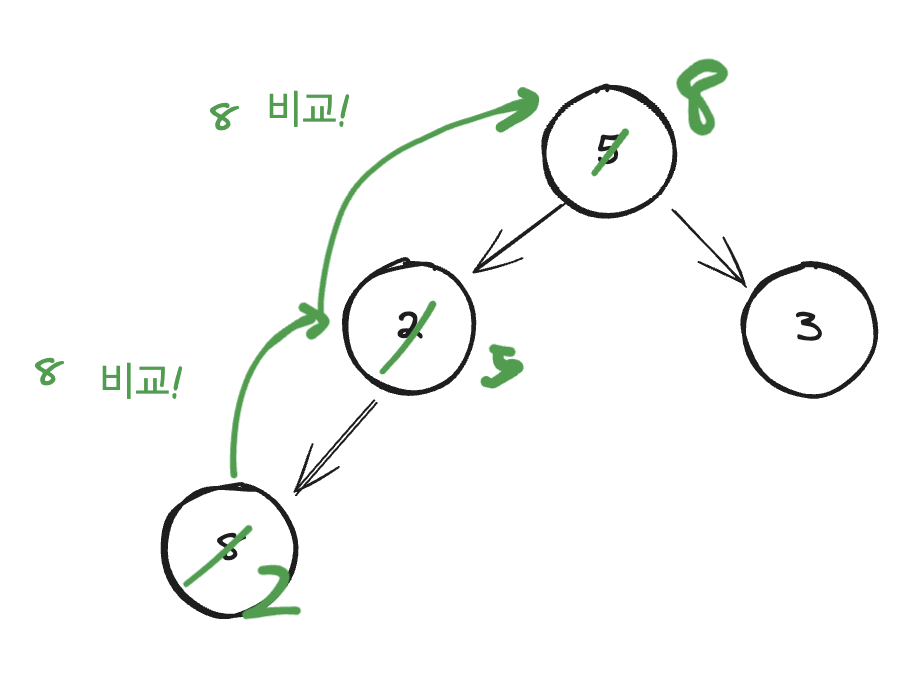
힙은 자식 노드의 값이 부모 노드의 값보다 크지만 않으면 그 구조가 성립한다. ( 값이 같아도 유지 된다. ) 그리고 heap에서 같은 레벨 노드의 Left와 Right 자식 노드 간의 비교는 진행하지 않는다.
힙의 삭제
삭제(pop) 연산 같은 경우 로직이 다음과 같다.
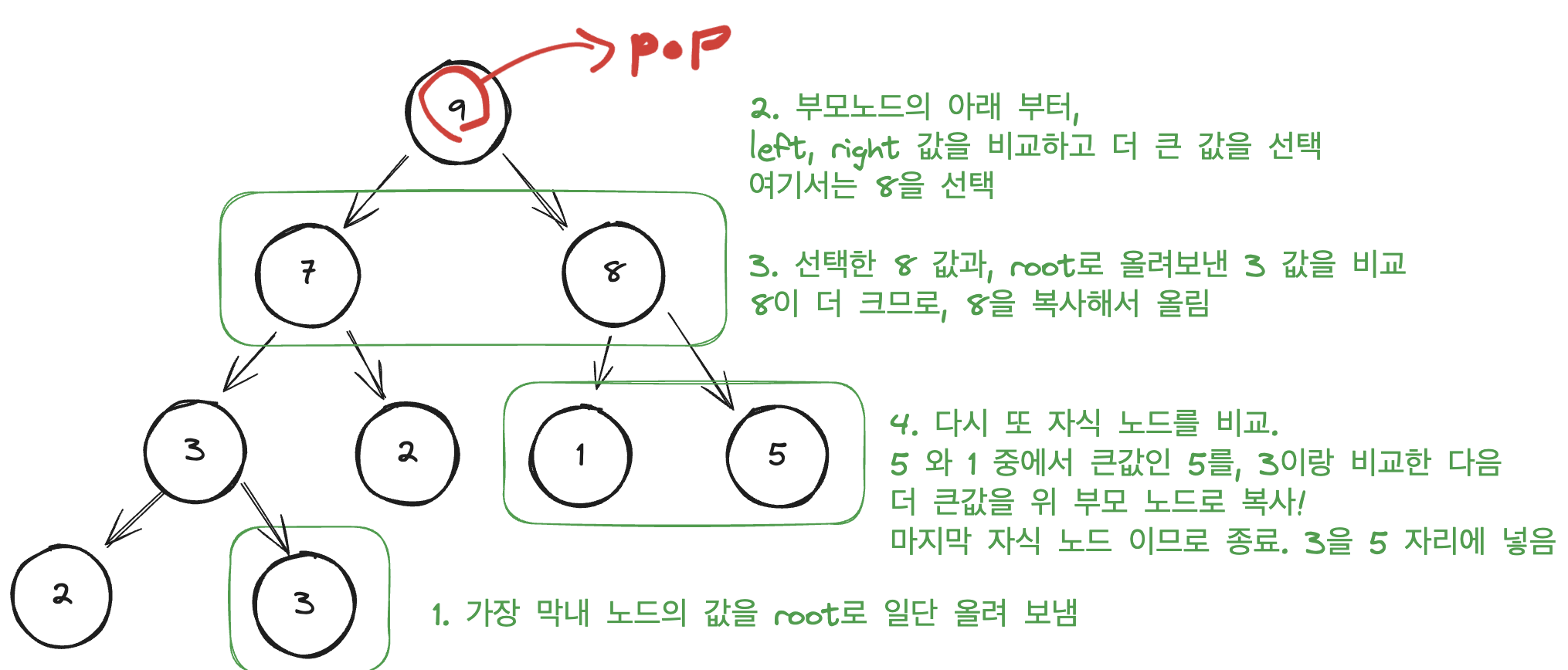
1. 가장 막내 노드의 값을 Root 노드로 일단 올려 보낸다. 위 그림에서는 2다.
2. 부모 노드를 시작으로, 자식 노드 left/right 값을 비교한 다음 더 큰 값과 올려보낸 값을 비교한다.
3. 위 예시에서는 3과 8중에 8이 더 크므로, 8을 부모노드 자리에 복사해서 올려 보낸다.
4. 이제 3과 8번 자식 노드 중에 큰 값을 비교하고, 올려 보낼지 말지 확인한다.
5. 막내 노드였던 3의 값이 더 큰 경우가 나올 때까지 반복하고, 막내 노드의 값이 더 크거나, 마지막 자식 노드까지 비교를 끝냈으면 값을 대입하고 종료한다.
시간 복잡도
설명을 잘 한것 같지는 않으나,, 위 설명이 모두 이해가 되었으면 힙의 삽입과 삭제 연산의 시간 복잡도를 잘 추측해 볼 수 있다. 먼저 삽입 연산은 시간 복잡도가 O(log n)이다. 마지막 자식 노드 자리에서 최악의 경우 맨 위의 부모노드까지 트리의 레벨만큼 비교 연산을 하기 때문에, 트리의 레벨이 n이라고 가정했을 때 O(log n)의 시간 복잡도를 가지고 있다.
삭제의 경우에도 마찬가지로 시간 복잡도는 O(log n)이다. 마지막 자식 노드를 부모 노드 위치로 올려 보낸다음에, 값이 더 큰 자식 노드와 값을 계속 비교해 나가고 이 연산 또한 최악의 경우 트리의 레벨만큼 연산을 하기 때문이다.
'Data Structure + Algorithm' 카테고리의 다른 글
| [자료구조] 기수 정렬(Radix Sort) (0) | 2024.08.05 |
|---|---|
| [자료구조] 머지 소트(Merge Sort, 합병 정렬) (0) | 2024.08.05 |
| [Algorithm] 최단 경로 찾기 - 다익스트라 알고리즘 (0) | 2023.06.07 |
| [Algorithm] 이진 탐색 정리 (0) | 2023.03.06 |
| [Algorithm] 그리디 알고리즘 정리 + 백준 추천 문제 (0) | 2023.02.28 |


