Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
Tags
- sql
- airflow
- redshift
- 가상환경
- S3
- HADOOP
- 운영체제
- dockerfile
- TIL
- 종류
- 컴퓨터네트워크
- Docker
- 파이썬
- 데이터 파이프라인
- 데이터엔지니어링
- 데이터 엔지니어링
- Django
- PYTHON
- 자료구조
- 정리
- 데이터 웨어하우스
- 데이터베이스
- AWS
- 컴퓨터 네트워크
- airflow.cfg
- TCP
- http
- 데브코스
- Go
- linux
Archives
- Today
- Total
홍카나의 공부방
[데이터베이스] 저장 구조 - 순차 방법(힙), B-Tree 본문
임시 저장해 둔 글이 3번이나 날라갔다......
의도치 않게 이 내용을 3번 이상 작성했다. 저장 잘하자.
데이터베이스의 저장 구조
- 데이터베이스 데이터의 용도에 맞게 적절하게 디스크에 저장할 필요가 있다.
- 그래서 가장 효율적인 저장구조를 선택하는 과정을 살펴본다.
- 이 과정은 DB의 쿼리 및 트랜잭션을 분석하여 데이터에 대한 접근 방식과 빈도를 고려하는 DB의 물리적 설계와 같다.
- 물리적 저장 장치에 데이터를 배치하고 접근하는 방법을 파일의 조직 방법이라고 한다.
- 파일 조직의 유형에는 순차 방법, 인덱스 방법, 해시 방법이 있는데 전부 살펴본다.
순차 방법

- 순차 방법의 대표적인 파일 유형으로는 힙 파일(heap file)이 있다.
- 레코드들이 삽입된 순서대로 파일에 저장된다.
- 힙 파일은 쉽다. 새로운 레코드의 삽입은 일반적으로 파일의 가장 끝에 삽입되며, 파일 중간에 반환된 빈 공간인 자유 공간에도 삽입될 수 있다.
- 원하는 레코드를 찾기 위해서는 모든 레코드들을 순차적으로 접근해야 한다. 최악의 경우 O(N)이 소요된다.
- 레코드들이 삭제된 후에는 빈 공간들을 회수해서 자유 공간에 반환한다.
인덱스 방법

- 인덱스 구조를 이용해서 데이터에 빠르게 접근하는 방법이다.
- 레코드들에 대한 포인터를 가지고 있는 인덱스 파일과, 실제 레코드를 저장하고 있는 파일인 데이터 파일로 구성된다.
B-Tree(Balanced Tree)

- 인덱스 방법으로 만들어진 대표적인 자료 구조로 B-Tree(균형 트리)가 있다.
- 균형 트리는 모든 리프 노드가 같은 레벨에 있다는 특징을 가지고 있다.
- 그리고 차수가 m인 B-트리의 특징으로 다음 2가지를 들 수 있는데
- 1) 루트 노드는 그 자체가 리프가 아닌 이상 적어도 2개의 서브트리를 가진다.
- 2) 내부 노드는 최소 ceil(m/2), 최대 m개의 서브트리를 가지고, 적어도 ceil(m/2) -1개의 키 값을 가진다.
B-Tree 노드의 구조와 특징

- B트리 노드는 다음과 같은 구조를 가지고 있는게 일반적이다.
- 여기서 n은 Key 값의 수 ( 1 <= n < m ), P는 서브트리에 대한 포인터, K는 키 값이다.
- 각 키 값은 그 키 값을 가지고 있는 레코드에 대한 포인터 A를 함께 가지고 있다.
- 한 노드에 있는 키 값들은 오름차순으로 구성되어 있다.
- 특정 키 값의 왼쪽 포인터가 가리키는 서브트리의 모든 노드들의 키 값은 특정 키 값보다 작다.
- 반대로 오른쪽은 크다! 이진 탐색 트리(BST)를 들어본 사람이라면 느낌이 오는 특징이다.
B-Tree의 연산(1) - 탐색
- 먼저 B-트리에서 직접 탐색은 빠르다. 키 값에 의한 분기로 타고 타고 내려가서 찾으면 끝. 밑이 m인 O(logN)이 걸린다.
- 다만 순차 탐색은 중위 순회(Inorder Traversal, L-V-R)로 진행되는데, 직접 탐색보다 느리다.
- 그래서 B-Tree는 특정한 값을 검색하는데 최적화되어 있다.
- 순차적으로 모든 키 값을 탐색하려면 .. 느리다! 재귀를 사용하니까 메모리 잡아먹고... 느려지고.. 뭐 그렇다.
- 그래서 만약 DB 순차 검색을 해야하면.. 인덱스를 B-Tree로 짜는 것은 지양해야 한다.
B-Tree의 연산(2) - 삽입
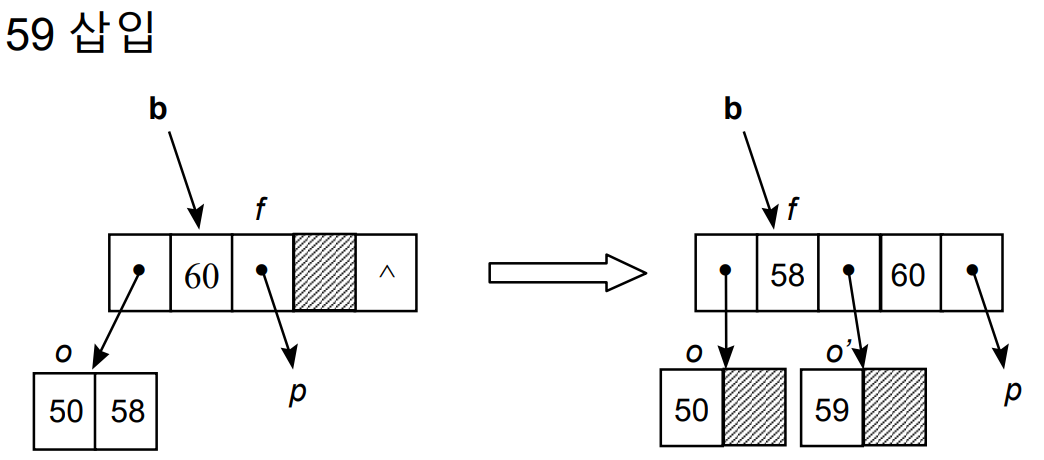
- 트리의 균형을 유지하고, 노드의 키 값은 오름차순이라는 제약조건을 유지하면서 삽입을 해야 한다.
- 1) 리프 노드에서 삽입은 빈 공간이 있는 경우 단순히 빈 공간에 삽입한다.
- 2) 만약 빈 공간이 없는 경우, Overflow가 발생하므로 노드가 분할되어야 한다.
- 2-1) ceil(m/2)번째의 키 값을 부모노드로 올린다.
- 2-2) 나머지는 반씩 나눈다. (왼쪽, 오른쪽 서브트리로)
- 2-3) 만약 부모 노드로 ceil(m/2)번째 키 값을 올렸는데 부모 노드도 오버플로우라면, 부모 노드도 분할한다.
- 만약 노드 overflow 때문에 루트 노드까지 올라갔는데 루트 노드도 꽉 차있다면, 루트 노드도 분할되고, Tree의 Depth가 하나 더 증가하게 된다.
B-Tree의 연산(3) - 삭제

- 모든 키의 삭제는 리프 노드에서 이루어진다.
- 그래서 만약 삭제하고자 하는 키 값이 리프 노드에 없다면, 그다음키 값과 자리 교체가 이루어진다.
- 만약 노드의 키 개수가 ceil(m/2) -1보다 작아진다면, (3차에서는 2-1 =1이므로 1보다 작은 0인 경우다.) 언더플로우가 발생한다.
- 언더플로우를 처리하는 방법은 1)재분배, 2)합병이 있다.
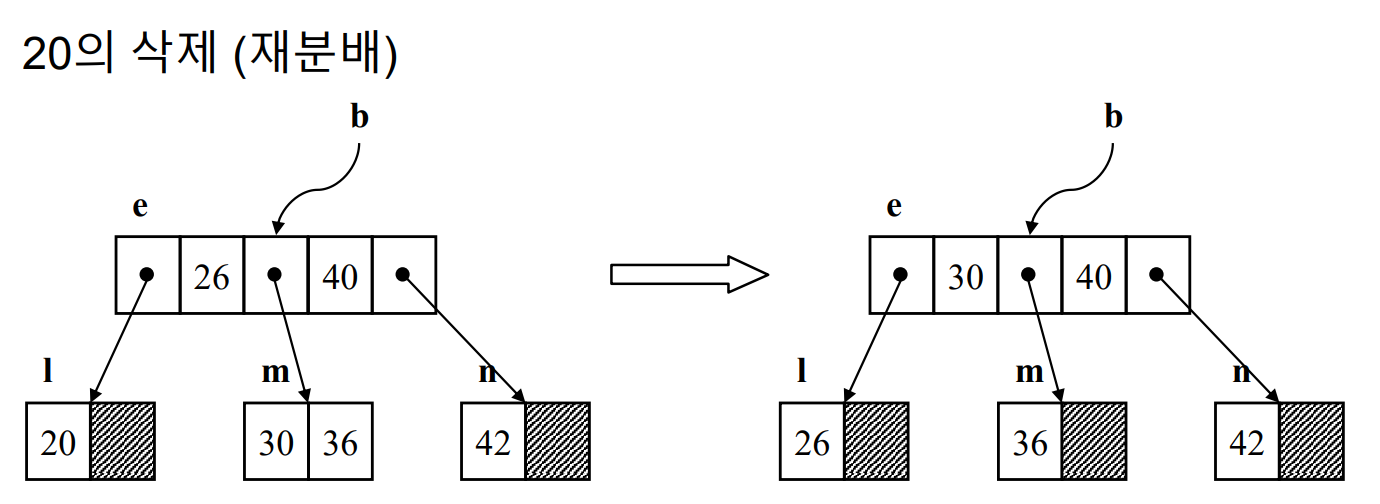
- 재분배는 형제 노드에서 키를 빼서 배치하는 방법이다. 이때 부모 노드의 키가 해당 노드로 이동하며, 차출된 키는 부모 노드로 이동한다. (즉, 키 값이 오름차순이라는 규칙을 깨지 않기 위해서다.)
- 위 예시에서 20이 삭제되었을 때나, 42가 삭제되었을 때 각각 30, 36이 부모 노드로 대체된다.

- 합병은 재분배가 불가능할 때(형제 노드들이 모두 최소의 키 값만 가질 때) 발생한다.
- 삽입에서 사용한 분할 과정과 정반대로 동작한다.
- 삭제 대상 노드의 오른쪽(또는 왼쪽) 형제 노드에 위치한 키 값들과 부모노드 키 값을 모아서 진행한다.
- B-Tree의 경우 삽입/삭제 연산이 그렇게 까지 비싼 연산은 아니다.
반응형
'Data Engineering > Database' 카테고리의 다른 글
| [데이터베이스] 삭제 : DELETE vs DROP vs TRUNCATE (0) | 2023.05.20 |
|---|---|
| [데이터베이스] 저장 구조 - 해싱 방법, 저장 구조의 비교 (0) | 2023.05.18 |
| [데이터베이스] B+Tree, 인덱스의 종류 (1) | 2023.05.18 |
| [데이터베이스] 하드 디스크의 구조 (0) | 2023.05.14 |
| [데이터베이스] 릴레이션, 스키마, 관계형 데이터베이스 개요와 SQL (0) | 2023.05.08 |




