| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 운영체제
- S3
- HADOOP
- Go
- 자료구조
- airflow
- http
- 가상환경
- Docker
- 데이터 웨어하우스
- 데이터엔지니어링
- AWS
- 종류
- linux
- airflow.cfg
- TCP
- PYTHON
- redshift
- 정리
- TIL
- 데이터 엔지니어링
- sql
- 컴퓨터 네트워크
- Django
- 데브코스
- 컴퓨터네트워크
- 데이터 파이프라인
- 파이썬
- dockerfile
- 데이터베이스
- Today
- Total
홍카나의 공부방
[강화학습] 3강 학습 노트 - Planning by DP 본문
Planning -> MDP가 어떻게 동작하는지 알 때 최적의 policy를 찾는 문제!
What is Dynamic Programming?
- 큰 문제를 작은 문제로 나눠서 해결하는 방법
- 작은 문제에 대한 솔루션을 찾고, 큰 문제를 해결하는 방법론 ( 학부에서 알고리즘 수업을 들었으면, 바로 알만한 방법 )
- Optimal Substructure가 필요하다.
- subproblem들이 Overlapping 해야 한다. ( soultion들을 분할-정복 방법처럼 reuse할 수 있어야 한다. )
Prediction vs. control:
- Prediction은 MDP <S,A,P,R,gamma>와 정책Pi를 input으로 준다.
- 그래서 가치 함수 V_pi를 찾는 것이다.
- control은 MDP <S,A,P,R,gamam>를 input으로 줬을 때 최적의 가치함수 또는 최적의 정책을 찾는 것이다.

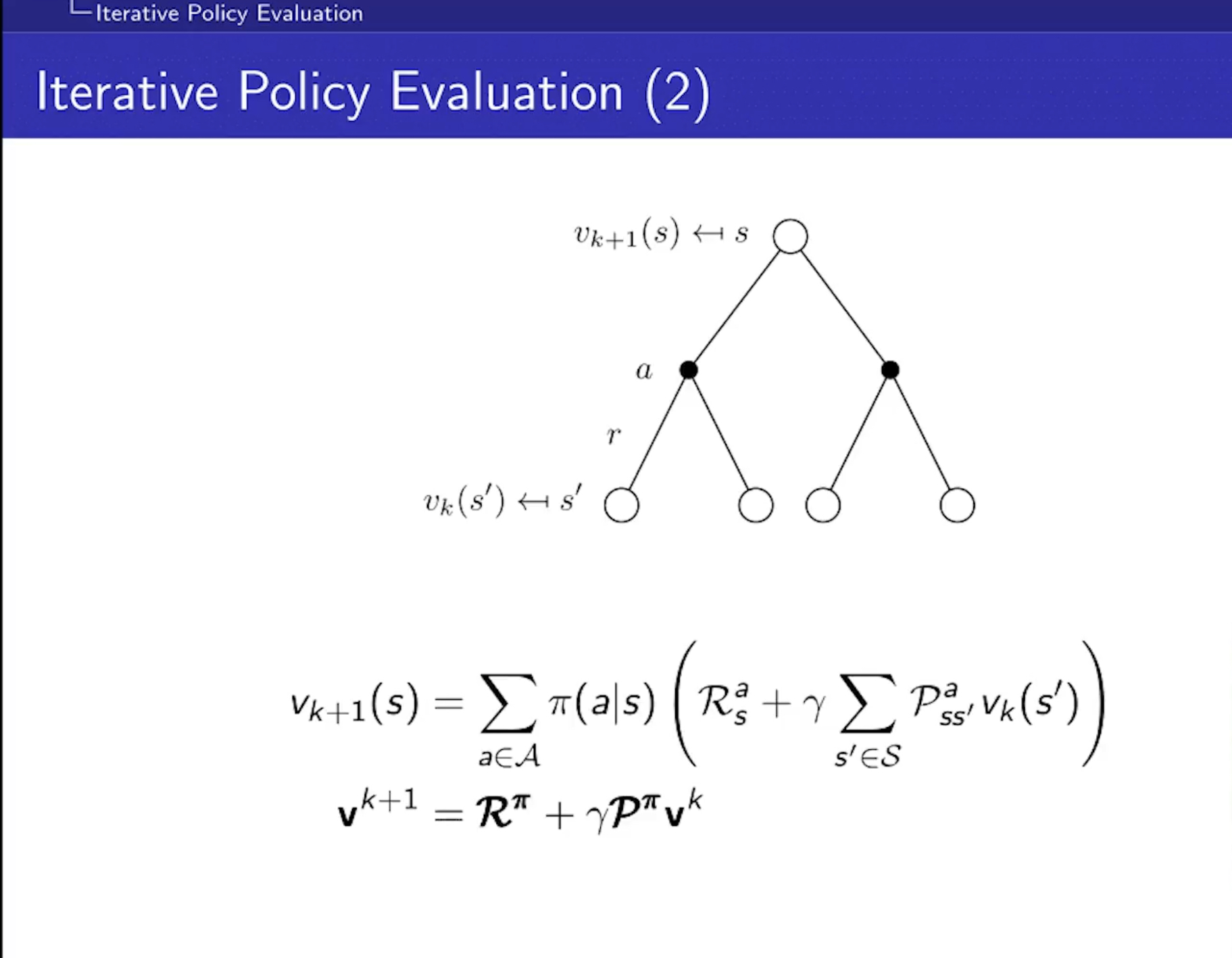
Policy Evaluation
- 정책을 평가한다는 것은 정책을 따라갔을 때 return(Value Function)이 얼마나 되냐? 를 알아가는 것
- Bellman Expectation을 이용해서 반복적으로 평가할 것
- synchronous backups를 사용한다.
- 처음에는 dummy value가 들어가더라도, 아래처럼 반복적으로 하면 결국 가치함수로 수렴한다는 것이 '증명'됨. 희한하네..
- MDP에 대한 모든 정보를 알기 때문에 벨만 기대 방정식을 사용할 수 있다.
Iterative Policy Evaluation in Small Gridworld
- Gridworld의 예시를 바탕으로 Planning이 풀려가는 예시임.
- terminal state의 값이 0.0으로 고정되는 이유는 가치 v(s)의 정의가 미래에 받게 될 누적 보상의 기댓값이기 때문.
- 맨 마지막 상태에는 '미래'라는 것이 존재하지 않기 때문에 항상 0이됨.
- 모든 문제에서 이게 가능함. (진짜?)

- k를 inf까지 갈 필요 없이 k=10만 되도 최적의 Policy까지 찾을 수 있다.
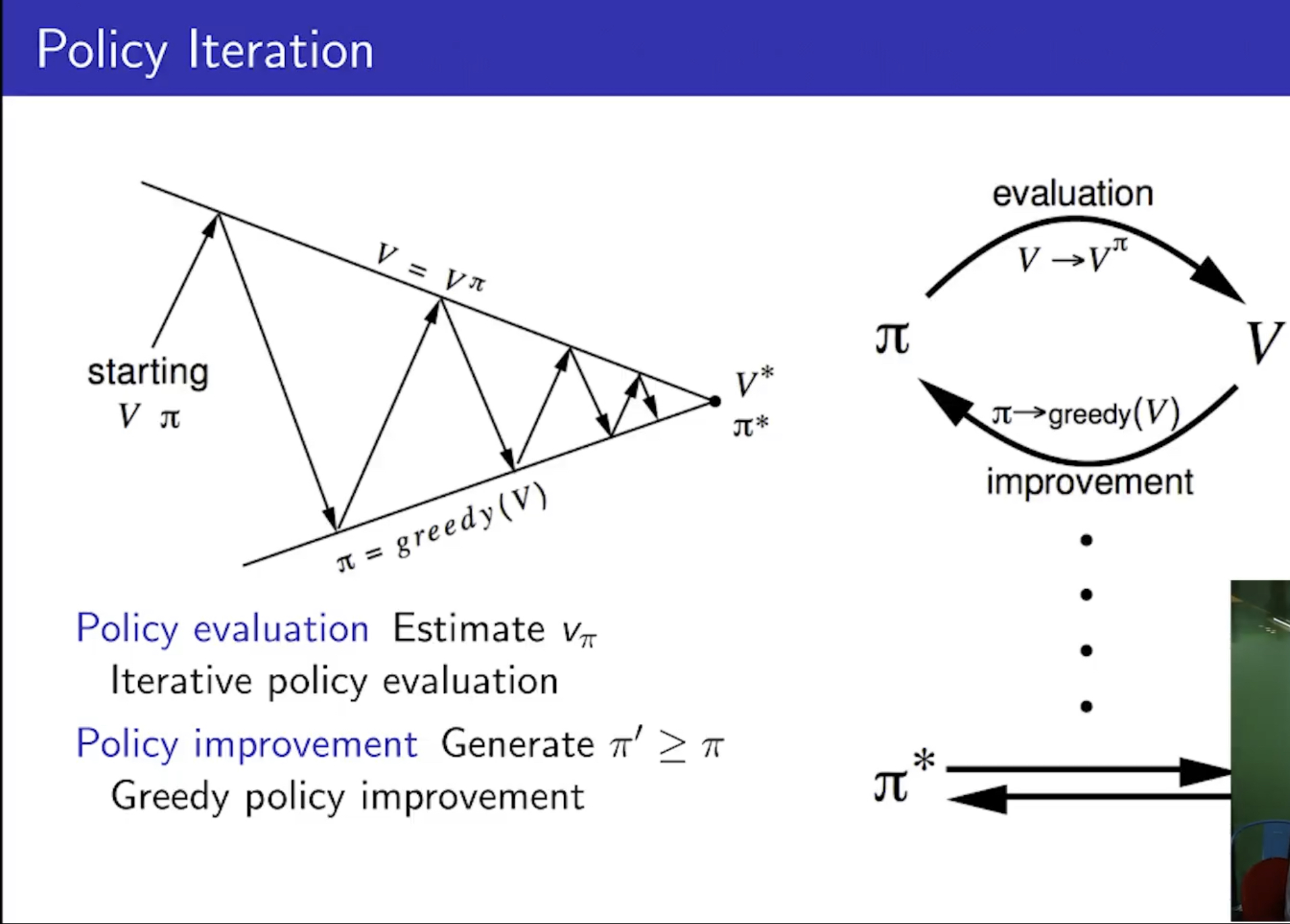
How to Improve a Policy
- Evaluate와 Improve를 반복함.
- 일반적으로는 improve와 Evaluate를 여러 번 거쳐야 한다.
- 이거를 반복하는 것이 Policy Iteration이다.
Value Iteration
- 밸류 이터레이션은 오로지 최적 정책이 만들어내는 최적 밸류 하나를 바라본다.
- 최적 정책이란 보상을 가장 많이 받을 수 있는 가장 좋은 정책, 이때 정책을 따라갔을 때 받는 밸류를 Optimal Value라고 한다.
- Policy Iteration과 다르게, Policy가 없다.
Why Optimal Value?
- 우리의 목적은 최적 정책을 찾는 것인데 왜 최적 밸류를 구했을까?
- MDP를 모두 아는 상황에서는 일단 최적 밸류를 알면, 최적 정책을 얻을 수 있기 때문이다.
- 에이전트 입장에서는 최적 밸류가 가장 높은 방향을 따라가면 끝.

- 시간 복잡도가 iteration마다 매우 높아서, 작은 문제에서만 사용할 수 있는 방법.
- 계산 비용을 많이 줄일 수 있는 비동기적 DP에 대해서는 추후에 배운다.
'AI > Reinforcement Learning' 카테고리의 다른 글
| hey chatGPT, 강화학습을 배우려면 어떻게 해야해? (0) | 2022.12.06 |
|---|---|
| [강화학습] 4강 - Model-Free Prediction (0) | 2022.12.04 |
| [강화학습] 2강 학습 노트 - Markov Decision Process (0) | 2022.11.28 |
| [강화학습] 기초 이론 1강 학습노트 (0) | 2022.11.26 |




