| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 데이터 웨어하우스
- airflow
- PYTHON
- Go
- 파이썬
- S3
- 데이터 엔지니어링
- 운영체제
- http
- 컴퓨터네트워크
- TIL
- redshift
- 자료구조
- 데이터베이스
- 데이터 파이프라인
- 가상환경
- Docker
- 정리
- TCP
- airflow.cfg
- AWS
- Django
- HADOOP
- 데브코스
- dockerfile
- 종류
- linux
- 데이터엔지니어링
- sql
- 컴퓨터 네트워크
- Today
- Total
홍카나의 공부방
[강화학습] 2강 학습 노트 - Markov Decision Process 본문
2강에는 Markov Decision Process에 대해서 배운다.
Introduction to MDPs
- Markov decision processes는 강화학습을 위한 환경을 표현한다.
- Fully Observable임을 가정한다.
- 대부분의 강화학습 문제가 MDPs로 형식화할 수 있다.
- Partially observable problems도 MDPs로 전환 가능, Bandits 문제도 1가지 상태의 MDPs 문제임.
Markov Property
- 현재 State만 필요할 뿐, History는 던져버릴 수 있다.
State Transition Matrix
- 마르코프 프로세스에서는 action이 없기 때문에, S_t에서 S_t+1이 될 수 있는 여러 state로 전이될 수 있는 확률을 나타낸 것
- 행렬안에 원소는 각각 확률을 나타낸다.
- 원소의 갯수는 state가 n개가 있다면, P_nn까지 존재.

Markov Process
- Markov Process(혹은 Markov Chain)은 튜플 <S, P>로 정의할 수 있다.
- S는 state의 (유한한) 집합이다.
- P는 State Transition Probability Matrix이다. ( 상태 전이 확률 행렬이라고 번역하는게 맞나.. )
- 샘플링한다 = 확률변수로부터 event가 발생하여 terminate되기 까지 변화된 state들을 나타내는 episode들의 집합을 모은다.
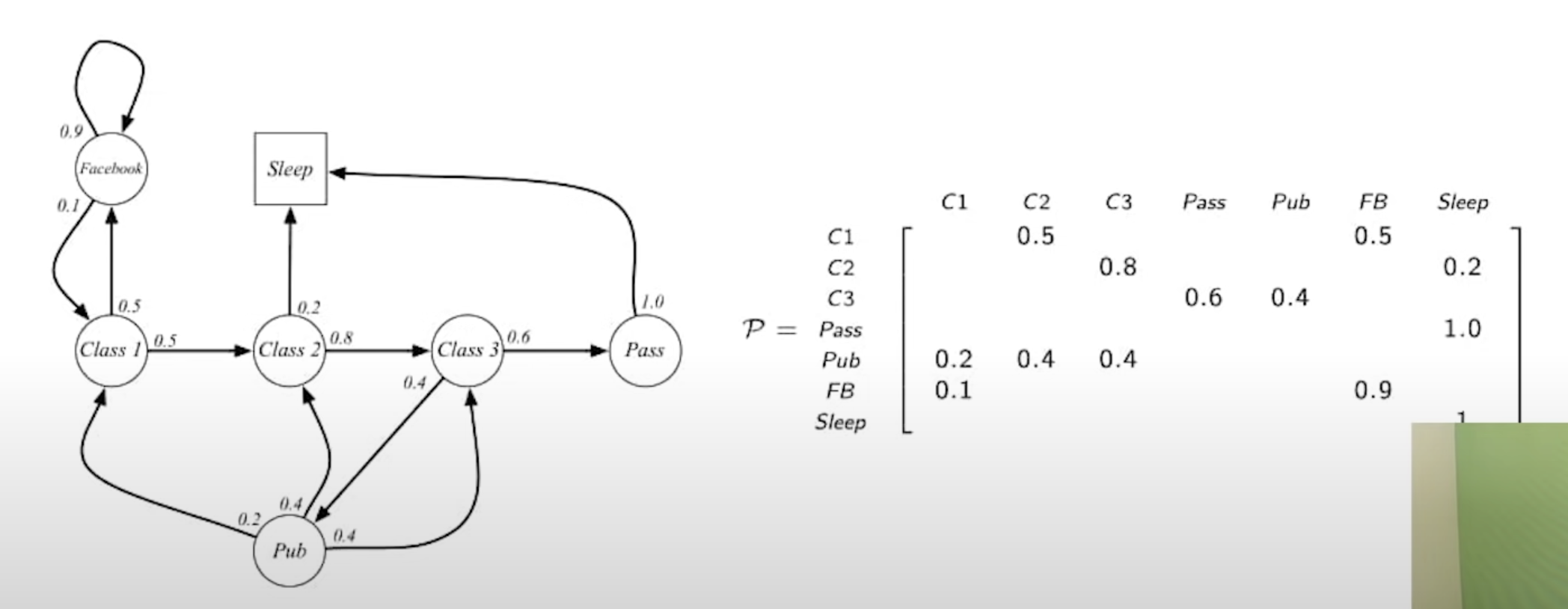
Markov Reward Process(MRP)
- 마르코프 보상 프로세스는 <S, P, R, r>이 추가된다.
- S는 state의 (유한한) 집합이다.
- P는 State Transition Probability Matrix이다. (상태 전이 행렬)
- reward는 리워드 함수로, 어떤 state에 도달하면 특정 reward 스칼라 값을 받는다 라는 것을 state별로 정리한 함수.
- gamma is discount factor, 0 <= r <= 1
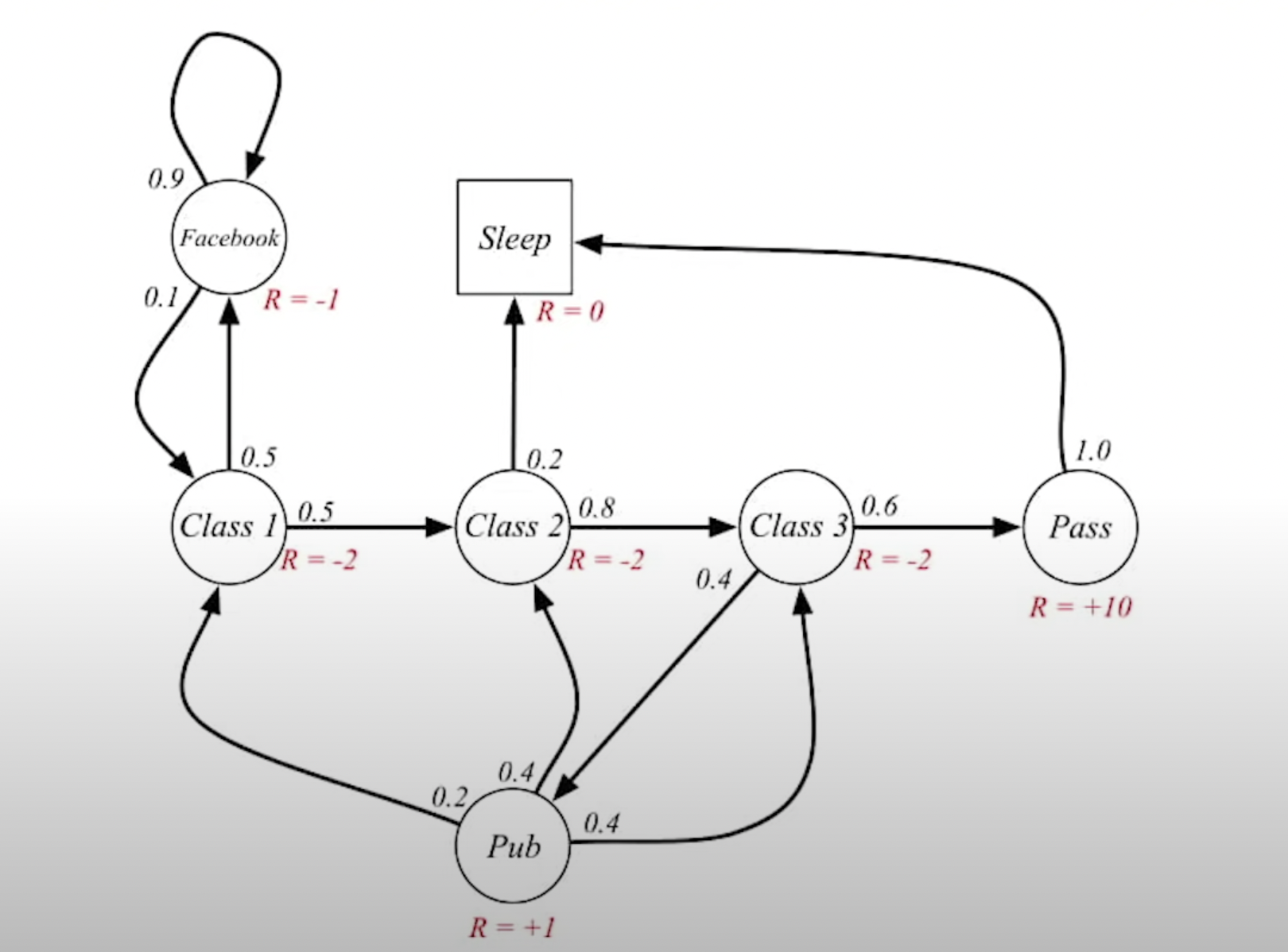
Student MRP Example
- Graph의 Edge로 가도 보상이 있는가? 없다. 리워드 프로세스에서는 action이라는 것이 없기 때문에.
- 오로지 확률적으로 특정 state에 도달하면 해당 state에 맞는 reward를 받게 된다.

Return
- 미래에 받는 reward는 gamma로 인해 할인이 되어 받게 된다.
- gamma가 0에 가까울수록 단기적인 보상을 추구, gamma가 1에 가까울수록 장기적인 보상을 추구.
- Cumulated return을 maximise하는 것이 강화학습의 목적!
Why discount?
- 마르코프 리워드나 디시젼 프로세스는 할인이 들어간다. 그 이유는..
- 수학적으로 편리하기 때문이다. 할인 때문에 수렴성이 증명이 된다.
- 심리적으로 사람은 즉각적인 보상을 선호하기 때문이다.
- 보상이 만약 재무적인 보상과 관련된다면, 즉각적인 보상은 지연된 보상에 비해 더욱 큰 이자를 벌 수 있을지도 모르기 때문이다.
- gamma가 1인 액면채 느낌으로 마르코프 보상 프로세스를 사용할 수도 있다. ( 무한히 갈 수 없는 process등..? )
- return이 무한이 되는 것을 피하기 위함.

Value Function(MRP)
- State가 s일 때, 샘플링을 진행해서 얻을 수 있는 Value의 기댓값. ( G_t는 확률변수 )
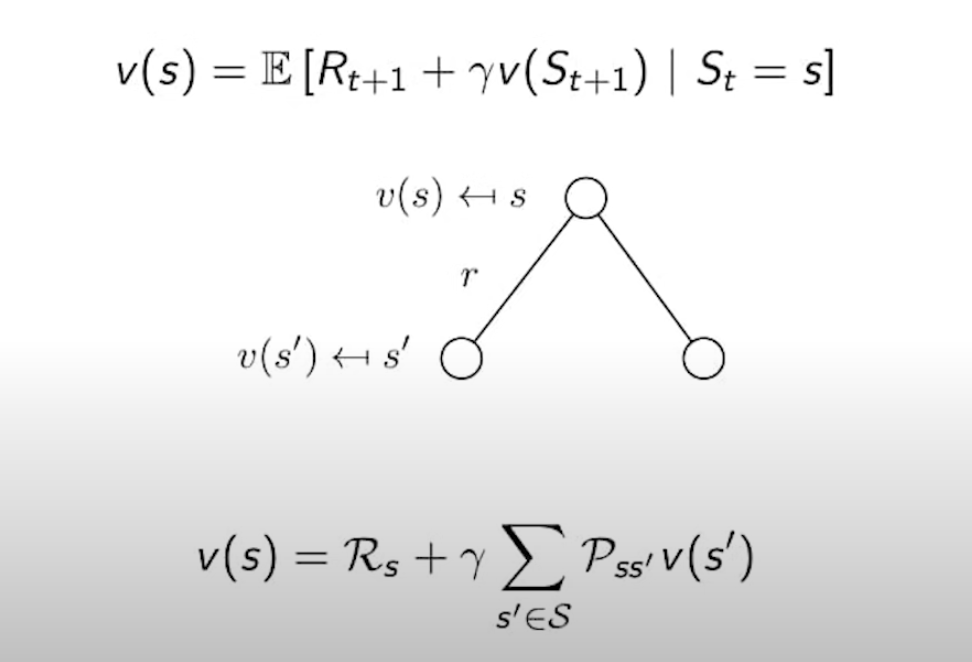
Bellman Equation for MRPs(벨만 방정식)
- value function은 Bellman Equation에 의해서 학습된다.

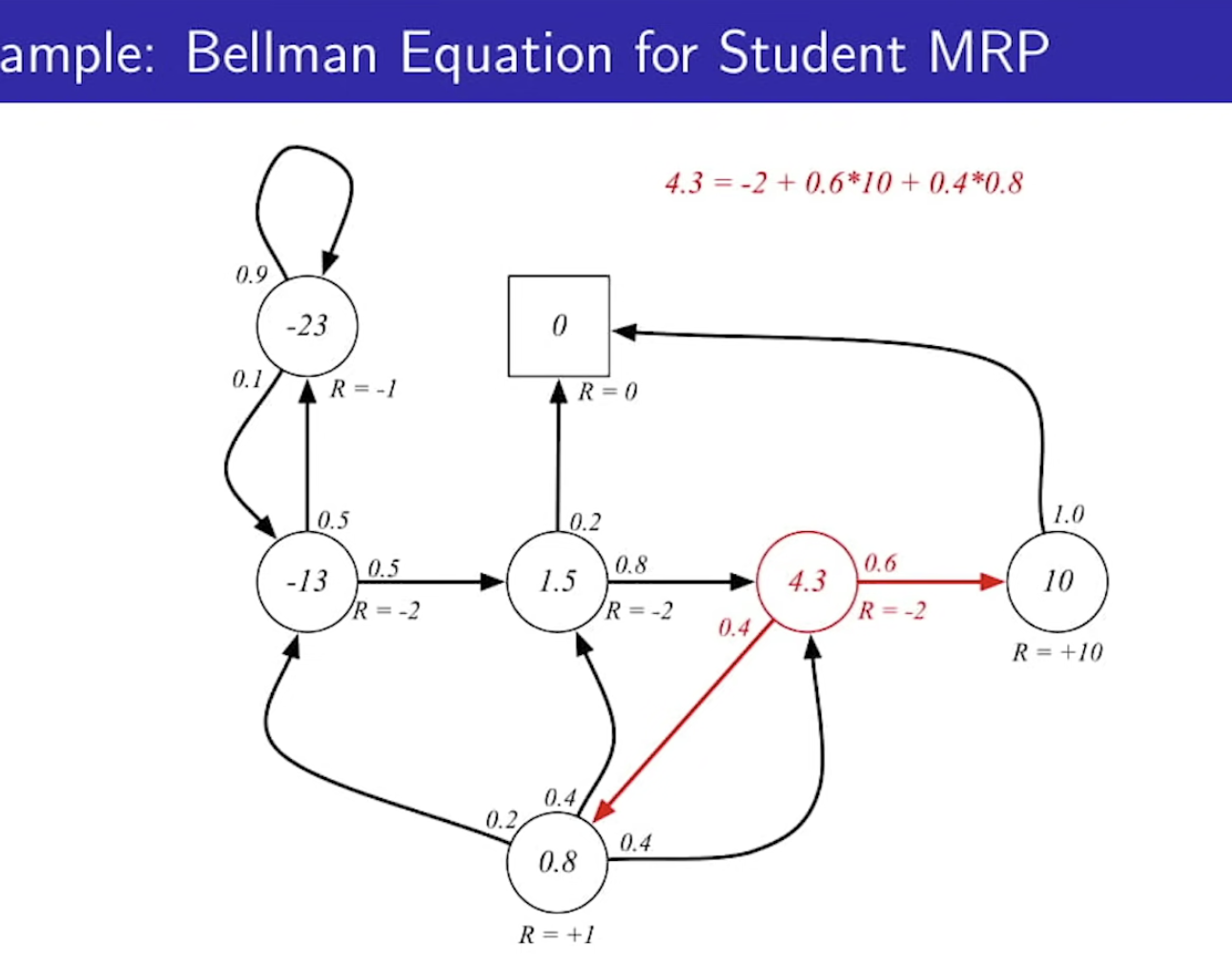
Bellman Equation for Student MRP
- value가 왜 4.3인지를 위 그림의 v(s)식을 바라보면서 이해해볼 것. (아마 gamma = 1이라고 가정)
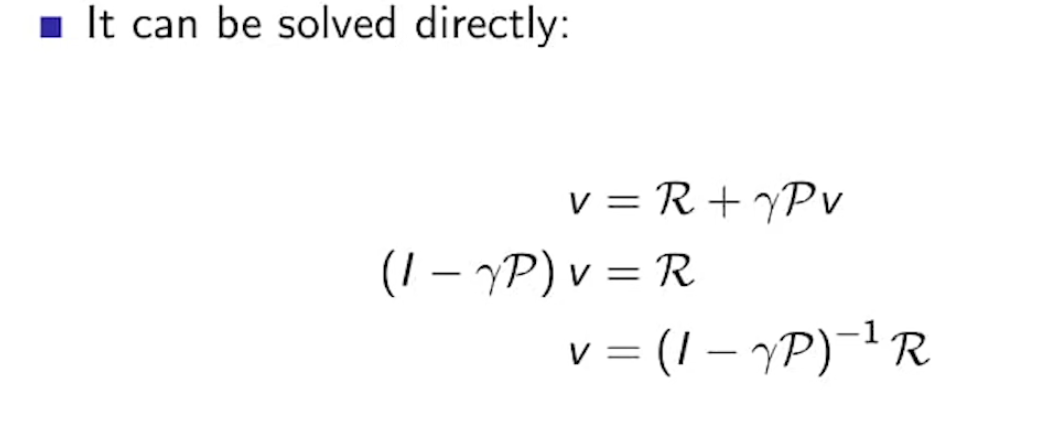
Solving the Bellman Equation
- 벨만 방정식은 선형 방정식이다.
- 작은 문제의 MRPs에 대해서는 한 방에 직관적으로 풀 수 있다.
- 큰 문제의 경우, 다이나믹 프로그래밍이나 몬테카를로 평가 등으로 해결해야 한다.
- 계산 복잡도가 O(n^3)기 때문에, state가 10,000개만 되어도 저 식으로 해결하기에는 매우 복잡하다.
Markov Decision Process(MDP)
- 마르코프 의사결정 프로세스는 <S, A, P, R, r>로 구성되어 있다.
- 유한한 집합의 Action이 추가된 것이 MRP와의 차이점이다.
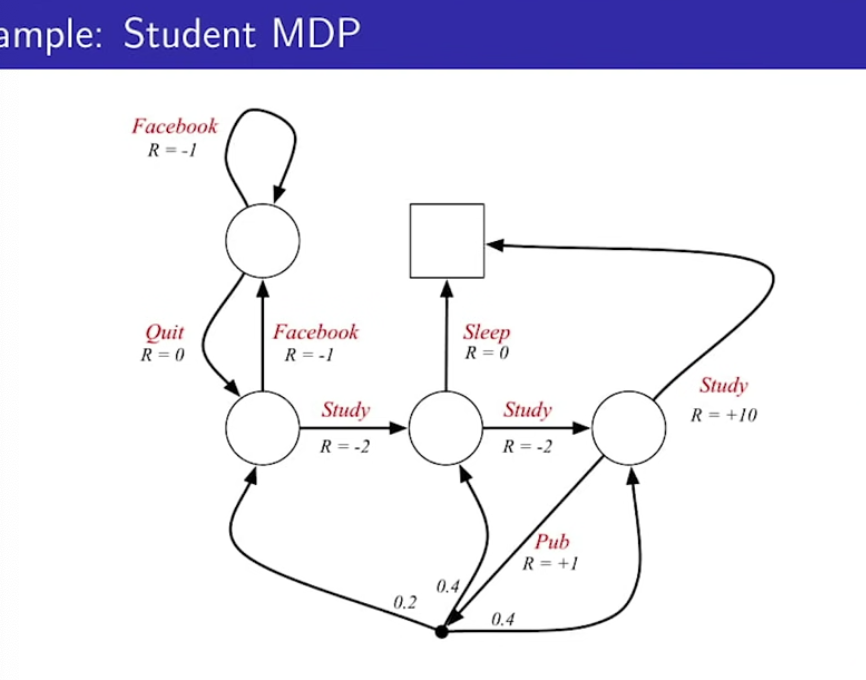
State의 이름이 사라지고 Action에 이름이 붙었다.
Policies (1)
- MRP에서는 Action이 없었으나 MDP에서는 Action을 어떤 정책을 가지고 하는지가 중요하다.
- Policy pi는 주어진 state에서 action을 행할 확률분포이다.
- 정책들은 정상성을 띄닌다. (시간 독립적임.)
- MDP 정책은 현재 상태에 의존한다. (history가 아닌)

Value Function
- MDP의 State-Value Function V_pi(S)에는 정책이 추가됨.
- sample들의 episode가 끝났을 때 얻을 수 있는 value들의 평균(기댓값)



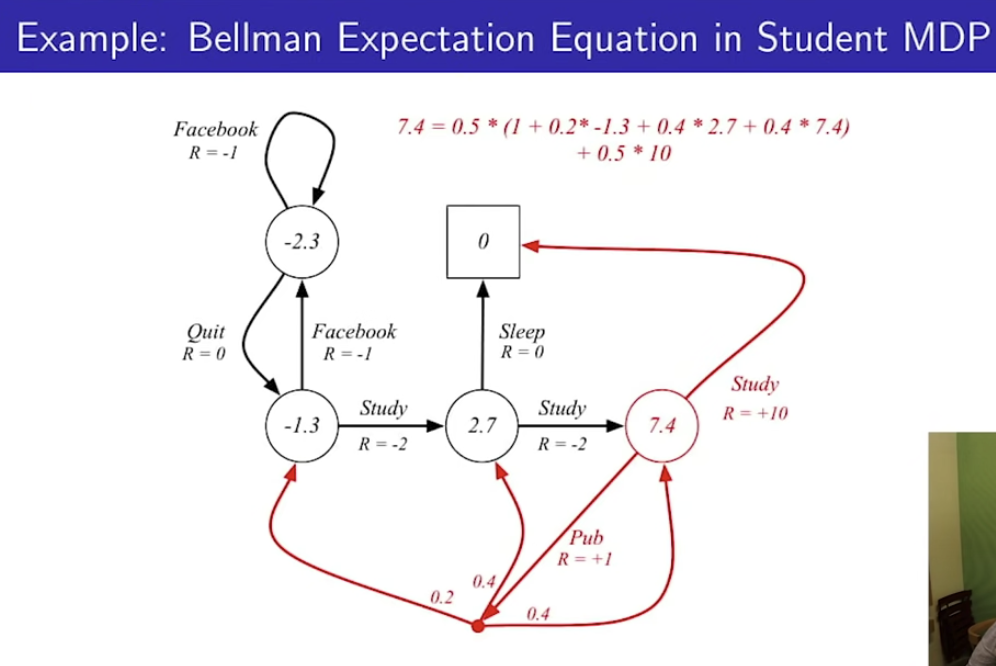
7.4라는 value값은
0.5 * 10 ( study를 하러 갈 때 받는 리워드 )
+ 0.5 * (1 + 0.2 * -1.3 + 0.4*2.7 + 0.4+7.4) <- Pub으로 간 이후 확률적으로 다음 state의 보상까지
( 위 그림에서는 확률을 1/2, 1/2로 가정 )
Optimal Value Function
- 가능한 모든 policy들에 대해서 가치 함수를 극대화 시키는 최적의 가치 함수
- 강화학습의 목적이 사실상 이 함수를 구하는 것
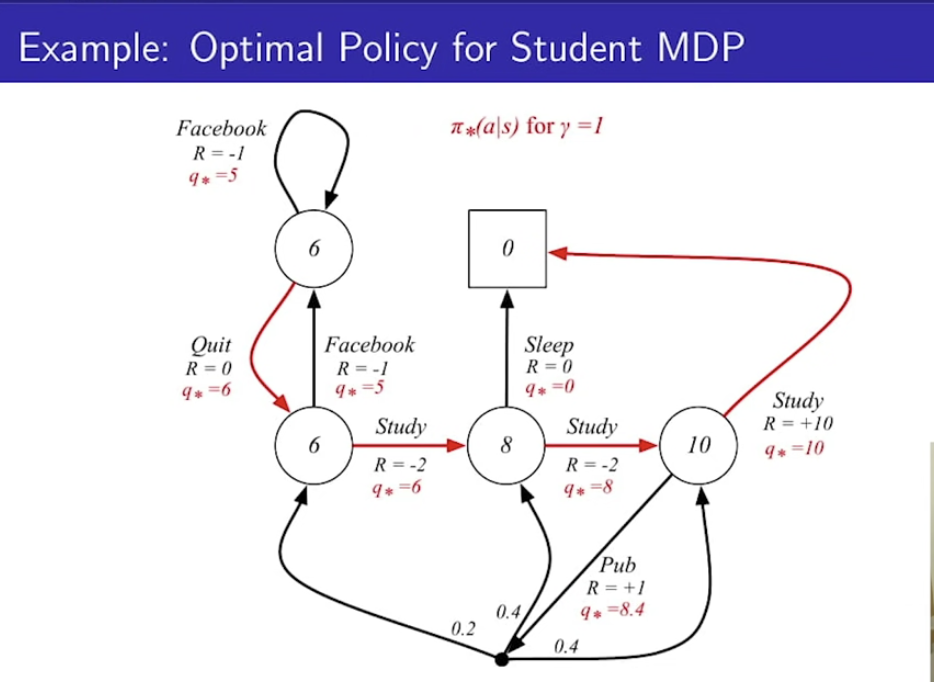
Optimal Policy
- 두 정책에 대한 비교, 어느 정책이 더 나은 것인가?

- 모든 MDP에 대해서, 최적의 정책 pi*는 존재한다.
- 해당 pi*는 모든 다른 정책보다 낫거나, 똑같다. (가치를 더 얻을수 있거나, 똑같다.)
- 모든 최적의 정책'들'은 최적의 가치 함수와 같다.
- 모든 최적의 정책'들'은 최적의 행동 가치 함수와 같다.
'AI > Reinforcement Learning' 카테고리의 다른 글
| hey chatGPT, 강화학습을 배우려면 어떻게 해야해? (0) | 2022.12.06 |
|---|---|
| [강화학습] 4강 - Model-Free Prediction (0) | 2022.12.04 |
| [강화학습] 3강 학습 노트 - Planning by DP (2) | 2022.12.04 |
| [강화학습] 기초 이론 1강 학습노트 (0) | 2022.11.26 |




